🎼 Lista de reproducción de Spotify de la newsletter
«Good statistical analysis is not a purely routine matter, and generally calls for more than one pass through the computer. The analysis should be sensitive both to peculiar features in the given numbers and also to whatever background information»
F. J. Anscombe (1973)
✉️ LA MISIVA: ¿por qué es tan importante la visualización de datos en estadística?
«Toxicidad fuera, mala correlación fuera, me llamas outlier, te doy la mano»
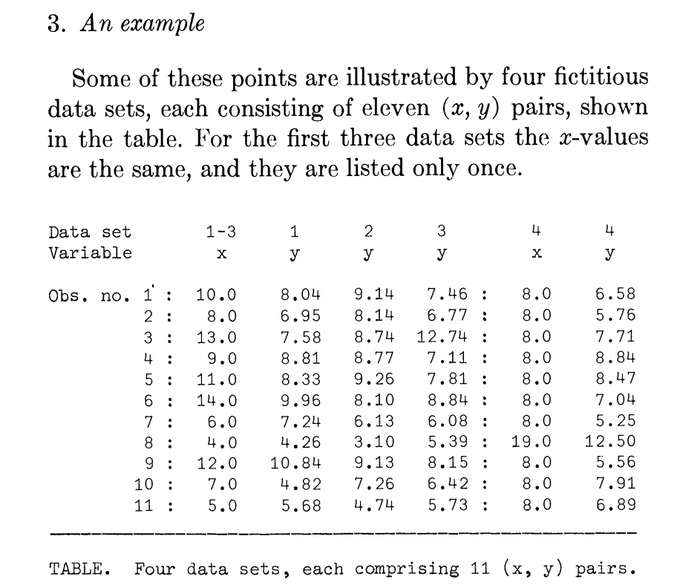
El cuarteto de Anscombe no tiene temazo de Ibai pero tiene historia: 4 pares de datos (X, Y) que, aún a día de hoy, nadie sabe como los generó F. J. Anscombe.
🗺 Un poco de contexto
Anscombe fue un estadístico inglés que trabajó en la épica Rothamsted Experimental Station, aquel sitio donde Fisher y Bristol realizaron el experimento del té con leche que dio lugar al famoso p-valor (te dejo la historia por aquí, ya hablaremos del p-valor en otra misiva). En 1963 publicó su trabajo más importante, sistematizando el análisis de errores, pero el artículo que nos atañe es el que publicó en 1973 [1], donde presentó en sociedad su famoso cuarteto.

💡 Para entenderlo: imagina que medimos la temperatura mínima🌡 durante 11 meses (11 valores) de 4 ciudades en 2020 (variable X) y volvemos a medir en las 4 ciudades en 2021 (variable Y):
Variable X (2020): 11 valores en cada una de las 4 ciudades.
Variable Y (2021): 11 valores en cada una de las 4 ciudades.
✅ 11 pares de variables, 4 grupos.
El ejemplo de las temperaturas tenía simplemente un propósito didáctico ya que Anscombe no midió nada, simplemente construyó los datos de forma artificial.
🔝 ¿Qué tiene de especial este conjunto de datos?
Como hemos dicho, tenemos en realidad 8 variables: {X1, X2, X3, X4} e {Y1, Y2, Y3, Y4}, de 11 valores cada una. Fíjate bien en ellas.
La media y varianza (cómo de dispersos están los datos respecto a la media) de todas las X es la misma.
La media y varianza de las Y es la misma.
La correlación (relación lineal) del par {X1, Y1} es 0.81, pero también es 0.81 la correlación de {X2, Y2} , la correlación de {X3, Y3} y la correlación de {X4, Y4}: si intentamos predecir Y a partir de X mediante un modelo de regresión lineal, ¡el modelo (la recta) sería el mismo!
🤯 TODOS los parámetros numéricos calculados son idénticos.
¿Es posible que las matemáticas nos digan que 4 pares de variables son idénticas pero… que no lo sean?
Sí, y eso es lo que Anscombe se propuso ilustrar. Y es que en estadística muchas veces hay una querencia a analizar datos SOLO de forma numérica, haciendo uso de las matemáticas, sin ni siquiera haberlos visualizado. Anscombe se propuso crear cuatro conjuntos de datos que pareciesen iguales pero que no lo fuesen, para así ilustrar la importancia de la visualización de datos (más allá de lo estético).

Y es que si te fijas en la gráfica superior, una vez pintados los 4 conjuntos de datos (azul - naranja - rojo - verde con 11 puntos cada uno), las variables no podían ser más distintas entre sí. Anscombe quería ilustrar la importancia en la estadística de la visualización de datos (que se lo digan a John Snow), y cómo un mero análisis numérico no siempre se suficiente: un visualización previa ya nos habría indicado por ejemplo que el conjunto verde y el naranja no puede ser modelizado con una recta (de hecho el verde es literalmente el mismo dato salvo uno a su aire).
🦖 Hablemos de dinosaurios
Quizás pienses que el caso anterior es una casualidad, y que nunca podría sucedernos en la vida real. Hace unos años el periodista y diseñador Alberto Cairo quiso llevar esta idea al límite, y se dispuso a crear el que ya se conoce como el conjunto de datos Datasaurus, una serie de pares de puntos representando algunas formas (círculos, elipses y cruces, entre otros). Todos ellos muestran patrones diferentes pero las principales características numéricas son las mismas.
¡Incluso la forma de un dinosaurio!

No he querido añadirlo porque ya tenéis suficiente fantasía visual pero no solo tienen la misma correlación sino que si pintamos para cada conjunto de la docena el ajuste lineal (la recta de regresión) sería la misma.
Las apariencias engañan, especialmente en estadística, y por eso es tan importante la visualización de datos. «No hay gráfico malo, solo cuentan distintas historias» dicen algunos. El problema es cuando la historia es de terror.
📰🧠 DATOS ESTOCÁSTICOS
Francis J. Anscombe era cuñado de otro ilustre, John W. Tukey, el creador del gráfico de cajas y bigotes [3].
Tukey también fue en 1947 la persona que acuñó el termino bit para referirse a la unidad mínima de información en computación («binary» + «digit») [4].
Para ingenieros/as: Tukey fue el co-creador del algoritmo FFT, que nos permite calcular de forma eficiente la transformada de Fourier (para muggles: la herramienta gracias a la cuál tienes Netflix o Spotify).
📖🔎 GLOSARIO
Medidas de centralización (media-mediana-moda): valores en torno a los que se concentran los datos. La más famosa es la media (aritmética) pero se perturba con valores extremos. La mediana es el valor «de en medio« si ordenamos de menor a mayor. La moda es el valor más repetido.
Medidas de dispersión: nos calibran la desviación de los datos respecto a ese centro. En general se usan respecto a la media (varianza, por ejemplo).
Medidas de posición: valores que nos permiten dividir los datos en partes iguales con el mismo porcentaje (percentiles, cuartiles, etc). Ejemplo: el percentil 35 es el número que nos deja por debajo el 35% y por encima el 65%; el percentil 81 nos deja por debajo el 81% y por encima el 19%.
📚 BIBLIOTECA
[1] Artículo «Graphs in Statistical Analysis» de F. J. Anscombe de 1973, donde mostró el cuarteto: [ARTÍCULO EN PDF]
[2] Entrada «Download the Datasaurus: Never trust summary statistics alone; always visualize your data» de A. Cairo de 2016, proponiendo el conjunto de datos Datasaurus: [LINK A LA ENTRADA]
[3] Libro «Exploratory Data Analysis» de J. Tukey de 1977, en el que usa por primera vez los gráficos de cajas y bigotes. [LIBRO ONLINE]
💡 PARA AMPLIAR SOBRE VISUALIZACIÓN
Paula Guisado, responsable del equipo de datos en RTVE.
Cédric Scherer, especialista en visualización de datos, y Dominic Royé, geógrafo y especialista en visualización de datos geográficos.
El arte del dato, cuenta especializada en ciencia y visualización de datos, administrada por Paula Casado.
Antonio Sánchez-Chinchón, matemático y creador de obras de arte a partir de código en R.
Michela Lazzaroni, diseñadora y especialista en visualización de datos.
Aplicación «Draw my data» de R. Grant para crear tu propio conjunto de datos con el ratón y luego descargarte el archivo generado visualmente: [ENLACE DE LA APLICACIÓN]
Artículo «Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing» de J. Matejka y G. Fitzmaurice de 2006 sobre la visualización de datos: [ARTÍCULO EN PDF]
📦 PAQUETERÍA
Paquete datasauRus (conjunto de datos Datasaurus [2])
Paquete datasets (conjuntos de datos, entre ellos el cuarteto de Anscombe [1])
Hasta aquí. Gracias por leer y por estar. Si quieres y entra dentro de tus posibilidades, puedes contribuir al proyecto y formar parte de la comunidad en Patreon.
¿Me ayudas a que llegue a más gente reenviando esta newsletter?







